#include <lf/geometry/point.h>

Inheritance diagram for lf::geometry::Point:

Public Member Functions
	Point (Eigen::VectorXd coord)

dim_t	DimLocal () const override
	Dimension of the domain of this mapping.

dim_t	DimGlobal () const override
	Dimension of the image of this mapping.

base::RefEl	RefEl () const override
	The Reference element that defines the domain of this mapping.

Eigen::MatrixXd	Global (const Eigen::MatrixXd &local) const override
	Map a number of points in local coordinates into the global coordinate system.

Eigen::MatrixXd	Jacobian (const Eigen::MatrixXd &local) const override
	Evaluate the jacobian of the mapping simultaneously at `numPoints` points.

Eigen::MatrixXd	JacobianInverseGramian (const Eigen::MatrixXd &local) const override
	Evaluate the Jacobian * Inverse Gramian ( \( J (J^T J)^{-1}\)) simultaneously at `numPoints`.

Eigen::VectorXd	IntegrationElement (const Eigen::MatrixXd &local) const override
	The integration element (factor appearing in integral transformation formula, see below) at number of evaluation points (specified in local coordinates).

std::unique_ptr< Geometry >	SubGeometry (dim_t codim, dim_t i) const override
	Construct a new Geometry() object that describes the geometry of the `i`-th sub-entity with codimension=`codim`

std::vector< std::unique_ptr< Geometry > >	ChildGeometry (const RefinementPattern &ref_pattern, base::dim_t codim) const override
	the child geometry is just a copy of the point geometry

Public Member Functions inherited from lf::geometry::Geometry
virtual bool	isAffine () const
	element shape by affine mapping from reference element

virtual	~Geometry ()=default
	Virtual destructor.

Private Attributes
Eigen::VectorXd	coord_

Additional Inherited Members
Public Types inherited from lf::geometry::Geometry
using	dim_t = base::RefEl::dim_t

Protected Member Functions inherited from lf::geometry::Geometry
	Geometry ()=default

	Geometry (const Geometry &)=default

	Geometry (Geometry &&)=default

Geometry &	operator= (const Geometry &)=default

Geometry &	operator= (Geometry &&)=default

Related Symbols inherited from lf::geometry::Geometry
void	PrintInfo (std::ostream &o, const Geometry &geom, int output_ctrl=0)
	Diagnostic output operator for Geometry.

std::ostream &	operator<< (std::ostream &stream, const Geometry &geom)
	Operator overload to print a `Geometry` to a stream, such as `std::cout`

Detailed Description

Definition at line 10 of file point.h.

Constructor & Destructor Documentation

◆ Point()

lf::geometry::Point::Point ( Eigen::VectorXd coord )

inlineexplicit

Definition at line 12 of file point.h.

Member Function Documentation

◆ ChildGeometry()

std::vector< std::unique_ptr< Geometry > > lf::geometry::Point::ChildGeometry	(	const RefinementPattern &	ref_pattern,
		base::dim_t	codim ) const

overridevirtual

the child geometry is just a copy of the point geometry

Implements lf::geometry::Geometry.

Definition at line 30 of file point.cc.

References coord_, lf::base::RefEl::kPoint(), lf::geometry::RefinementPattern::NumChildren(), lf::geometry::RefinementPattern::RefEl(), and lf::base::RefEl::ToString().

◆ DimGlobal()

dim_t lf::geometry::Point::DimGlobal ( ) const

inlineoverridevirtual

Dimension of the image of this mapping.

Implements lf::geometry::Geometry.

Definition at line 16 of file point.h.

References coord_.

Referenced by Jacobian().

◆ DimLocal()

dim_t lf::geometry::Point::DimLocal ( ) const

inlineoverridevirtual

Dimension of the domain of this mapping.

Implements lf::geometry::Geometry.

Definition at line 14 of file point.h.

◆ Global()

Eigen::MatrixXd lf::geometry::Point::Global ( const Eigen::MatrixXd & local ) const

overridevirtual

Map a number of points in local coordinates into the global coordinate system.

Parameters

local A Matrix of size DimLocal() x numPoints that contains in its columns the coordinates of the points at which the mapping function should be evaluated.

Returns: A Matrix of size DimGlobal() x numPoints that contains the mapped points as column vectors. Here numPoints is the number of columns of the matrix passed in the local argument.
\[ \mathtt{Global}\left(\left[\widehat{x}^1,\ldots,\widehat{x}^k\right]\right) = \left[ \mathbf{\Phi}_K(\widehat{x}^1),\ldots,\mathbf{\Phi}_K(\widehat{x}^k)\right]\;,\quad \widehat{x}^{\ell}\in\widehat{K}\;, \]
where \(\mathbf{\Phi}\) is the mapping taking the reference element to the current element \(K\).

This method provides a complete description of the shape of an entity through a parameterization over the corresponding reference element = parameter domain. The method takes as arguments a number of coordinate vectors of points in the reference element. For the sake of efficiency, these coordinate vectors are passed as the columns of a dynamic matrix type as supplied by Eigen.

For instance, this method is used in lf::geometry::Corners()

inline Eigen::MatrixXd Corners(const Geometry& geo) {

return geo.Global(geo.RefEl().NodeCoords()); }

lf::base::RefEl::NodeCoords

const Eigen::MatrixXd & NodeCoords() const

Get the coordinates of the nodes of this reference element.

Definition ref_el.h:241

lf::geometry::Geometry

Interface class for shape information on a mesh cell in the spirit of parametric finite element metho...

Definition geometry_interface.h:21

lf::geometry::Geometry::RefEl

virtual base::RefEl RefEl() const =0

The Reference element that defines the domain of this mapping.

lf::geometry::Geometry::Global

virtual Eigen::MatrixXd Global(const Eigen::MatrixXd &local) const =0

Map a number of points in local coordinates into the global coordinate system.

lf::geometry::Corners

Eigen::MatrixXd Corners(const Geometry &geo)

The corners of a shape with piecewise smooth boundary.

Definition geometry_interface.h:261

Additional explanations in Lecture Document Paragraph 2.7.5.17.

Implements lf::geometry::Geometry.

Definition at line 4 of file point.cc.

References coord_.

◆ IntegrationElement()

Eigen::VectorXd lf::geometry::Point::IntegrationElement ( const Eigen::MatrixXd & local ) const

overridevirtual

The integration element (factor appearing in integral transformation formula, see below) at number of evaluation points (specified in local coordinates).

Parameters

local A Matrix of size DimLocal() x numPoints that contains the evaluation points (in local = reference coordinates) as column vectors.

Returns: A Vector of size numPoints x 1 that contains the integration elements at every evaluation point.

For a transformation \( \Phi : K \mapsto R^{\text{DimGlobal}}\) with Jacobian \( D\Phi : K \mapsto R^{\text{DimGlobal} \times \text{DimLocal}} \) the integration element \( g \) at point \( \xi \in K \) is defined by

\[ g(\xi) := \sqrt{\mathrm{det}\left|D\Phi^T(\xi) D\Phi(\xi) \right|} \]

More information also related to the use of lovcal quadrature rules is given in Lecture Document Paragraph 2.7.5.24.

Implements lf::geometry::Geometry.

Definition at line 19 of file point.cc.

◆ Jacobian()

Eigen::MatrixXd lf::geometry::Point::Jacobian ( const Eigen::MatrixXd & local ) const

overridevirtual

Evaluate the jacobian of the mapping simultaneously at numPoints points.

Parameters

local A Matrix of size DimLocal x numPoints that contains the evaluation points as column vectors

Returns: A Matrix of size DimGlobal() x (DimLocal() * numPoints) that contains the jacobians at the evaluation points.

This method allows access to the derivative of the parametrization mapping in a number of points, passed as the columns of a dynamic matrix. The derivative of the parametrization in a point is a Jacobian matrix of size ‘DimGlobal() x DimLocal()’. For the sake of efficiency, these matrices are stacked horizontally and returned as one big dynamic matrix. Use Eigen's ‘block()’ method of Eigen::MatrixXd to extract the individual Jacobians from the returned matrix.

Implements lf::geometry::Geometry.

Definition at line 10 of file point.cc.

References DimGlobal().

◆ JacobianInverseGramian()

Eigen::MatrixXd lf::geometry::Point::JacobianInverseGramian ( const Eigen::MatrixXd & local ) const

overridevirtual

Evaluate the Jacobian * Inverse Gramian ( \( J (J^T J)^{-1}\)) simultaneously at numPoints.

Parameters

local A Matrix of size DimLocal() x numPoints that contains the evaluation points as column vectors.

Returns: A Matrix of size DimGlobal() x (DimLocal() * numPoints) that contains the Jacobian multiplied with the Inverse Gramian ( \( J (J^T J)^{-1}\)) at every evaluation point.

Note: If DimLocal() == DimGlobal() then \( J (J^T J)^{-1} = J^{-T} \), i.e. this method returns the inverse of the transposed jacobian.

Example for recovering a single transposed inverse Jacobian.

If both dimensions agree and have the value D, then the method returns the transposed of the inverse Jacobians of the transformation at the passed points. These are square DxD matrices.

To retrieve the j-th inverse transposed Jacobian from the returned matrix, use the block methdod of Eigen (case (D = DimLocal()) == DimGlobal())

JacobianInverseGramian(local).block(0,i*D,D,D)

lf::geometry::Point::JacobianInverseGramian

Eigen::MatrixXd JacobianInverseGramian(const Eigen::MatrixXd &local) const override

Evaluate the Jacobian * Inverse Gramian ( ) simultaneously at numPoints.

Definition point.cc:14

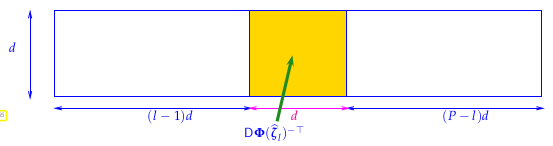
More explanations in Paragraph 2.8.3.14.

Implements lf::geometry::Geometry.

Definition at line 14 of file point.cc.

◆ RefEl()

base::RefEl lf::geometry::Point::RefEl ( ) const

inlineoverridevirtual

The Reference element that defines the domain of this mapping.

Implements lf::geometry::Geometry.

Definition at line 18 of file point.h.

References lf::base::RefEl::kPoint().

◆ SubGeometry()

std::unique_ptr< Geometry > lf::geometry::Point::SubGeometry	(	dim_t	codim,
		dim_t	i ) const

overridevirtual

Construct a new Geometry() object that describes the geometry of the i-th sub-entity with codimension=codim

Parameters

codim	The codimension of the sub-entity (w.r.t. `DimLocal()`)
i	The zero-based index of the sub-entity.

Returns: A new Geometry object that describes the geometry of the specified sub-entity.

Let \( \mathbf{\Phi} : K \mapsto \mathbb{R}^\text{DimGlobal} \) be the mapping of this Geometry object and let \( \mathbf{\xi} : \mathbb{R}^{\text{DimLocal}-codim} \mapsto K\) be the first-order mapping that maps the reference element RefEl().SubType(codim,i) to the i-th sub-entity of RefEl(). I.e. for every node \( \mathbf{n_j} \) of RefEl().SubType(codim,i) it holds that \( \mathbf{\xi}(\mathbf{n_j}) = \) RefEl().NodeCoords(RefEl().SubSubEntity2SubEntity(codim, i, DimLocal()-codim, j)).

Then the geometry element returned by this method describes exactly the mapping \( \mathbf{\Phi} \circ \mathbf{\xi} \)

Implements lf::geometry::Geometry.

Definition at line 23 of file point.cc.

References coord_.

Member Data Documentation

◆ coord_

Eigen::VectorXd lf::geometry::Point::coord_

private

Definition at line 41 of file point.h.

Referenced by ChildGeometry(), DimGlobal(), Global(), and SubGeometry().

The documentation for this class was generated from the following files:

/__w/lehrfempp/lehrfempp/lib/lf/geometry/point.h
/__w/lehrfempp/lehrfempp/lib/lf/geometry/point.cc

Public Member Functions

Private Attributes

Additional Inherited Members

Detailed Description

Constructor & Destructor Documentation

◆ Point()

Member Function Documentation

◆ ChildGeometry()

◆ DimGlobal()

◆ DimLocal()

◆ Global()

◆ IntegrationElement()

◆ Jacobian()

◆ JacobianInverseGramian()

Example for recovering a single transposed inverse Jacobian.

◆ RefEl()

◆ SubGeometry()

Member Data Documentation

◆ coord_